.
Es wird das prinzipielle Schema der Kodierung vorgestellt und danach der Umfang der zu kodierenden Zeichen festgelegt.
Neben den bereits vorgestellten Kodierungssystemen gibt es solche, welche auf sog. diakritischen Zeichen aufbauen. Diakritische Zeichen sind dadurch gekennzeichnet, daß ihr Ausdruck keine automatische Weiterbewegung der Schreibposition bewirkt, so daß dieses Zeichen mit dem folgenden Zeichen übereinander gedruckt wird (Non-Spacing Characters, [Bor91, S. 5.11,]). ISO 6937 sieht hierzu (mindestens) 15 Zeichen vor, welche sich am Beispiel mit dem Folgezeichen ,,a`` folgendermaßen darstellen:
à á â ã a a å ä a å a a ? a a
ISO 10646 definiert über 60 solche Zeichen.
Es ist klar, daß ein System, welches diakritische Zeichen voranstellt, das Sortiekriterium nicht erfüllen kann.
Dies gilt auch für die entsprechenden LaTeX -Darstellungen:
\`{a} \'{a} \^{a} \~{a} \={a} \u{a} \.{a} \"{a} \H{a} \aa\ \c{a} \b{a} ? \d{a} \v{a}
Der hier gemachte Vorschlag geht deshalb einen grundsätzlich anderen
Weg. Er geht davon aus, daß sich zu jedem darzustellenden Zeichen ein
lateinisches Grundzeichen aus dem 7 bit ASCII-Zeichensatz finden läßt, von
dem es abgeleitet werden kann (oder wo diese Ableitung
definiert wird). Jedes Zeichen wird dargestellt als Grundzeichen
gefolgt von einem Erweiterungs- bzw.
Ableitungszeichen.
Die folgenden Kodierungen mögen dies verdeutlichen:
ä 
a", à 
a`, ...
Damit nun einerseits aber die Kodierung eindeutig ist, andererseits die Sortierbedinung eingehalten wird, müssen auch die Grundzeichen selbst durch zwei Zeichen dargestellt werden:
a 
a!, c 
c!, ...
Das Erweiterungszeichen ,,!`` wurde dabei so gewählt, daß das Grundzeichen,
selbst bei einer Sortierung nach den ASCII-Codes, stets vor allen
abgeleiteten Zeichen kommt. Als erstes folgen die deutschen Umlaute mit
dem Erweiterungszeichen ,,"``.
Als nächstes ist die kodierungstolerante Selektion mittels regulärer
Ausdrücke zu untersuchen. Wir nehmen zunächt den häufig anzutreffenden
Fall, daß Akzente einfach weggelassen werden. Selektiere ,,?`` genau
ein beliebiges Zeichen und durch [] eingeschlossene Zeichen genau eines
dieser Zeichen, dann selektiert die Anfrage
,,A!m!p!e?r!e!`` Ampere, Ampère, Ampére, Ampëre, ...
,,A!m!p!e[!`]r!e!`` Ampere, Ampère
,,A!m!p!e`r!e!`` Ampère
Speziell im Deutschen treten häufig die Ersatzdarstellungen für die Umlaute und ß auf. Selektiere ,,*`` null oder beliebig viele Zeichen, dann selektiert die Anfrage
,,G!r!u"s"e!`` Grüße
,,G!r!u!e!s!s!e!`` Gruesse
,,G!r!u[!"][es]["!]*e!`` Grüße, Gruesse, Gruße, Gruene Nuesse, ...
,,G!r!u[!"][es]["!][es]!*`` Grüße, Gruesse, Gruße, ...
Keine Anfrage liefert ohne Erweiterung der regulären Ausdrücke
(um den Oder-Operator ,,|``, z.B.:
,,G!r!u("s"|!e!s!s!)e!``)
sicher nur Grüße und Gruesse.
Diese Erweiterungen unterstützen aber viele Systeme nicht. Allerdings
besteht die Möglichkeit der Realisierung als vollständiges Oder,
was einer Anfrage ,,(G!r!u"s"e!|G!r!u!e!s!s!e!)``
entspräche.
Die Probleme mit den deutschen Umlauten bei der Anfrage sind allerdings unabhängig von dem hier behandelten Kodierungsverfahren zu sehen, da es keinen Unterschied macht, ob ein Zeichen durch einen Code oder durch zwei Codes repräsentiert ist.
Nachdem das Kodierungsschema festgelegt wurde, ist als nächstes zu klären, welche Zeichen kodiert werden sollen. Damit verbunden ist die Frage, welche Zeichen als Grundzeichen auftreten sollen und welche als Erweiterungszeichen.
Die Zeichenauswahl könnte nach einem der folgenden Kriterien erfolgen:
Es wird hier der Dringlichkeit wegen eine Verbindung aus LaTeX
und ISO 8859-Latin1 vorgeschlagen, wobei eine Erweiterung in Richtung
Unicode (lateinischer Teil) offen stehen sollte. Spezielle Berücksichtigung
sollten die griechischen Buchstaben finden, da sie häufig an der
Bildung feststehender Begriffe beteiligt sind (z.B.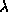 
-Kalkül).
Zunächst sind die Grundzeichen zu definieren. Ein Blick in ISO 10646 Group 0, Plane 1, Row 1 ergibt, daß fast alle Buchstaben außer b, f, m, p, q, v und x als Grundzeichen denkbar sind. Es werden also alle Buchstaben von a bis z und von A bis Z als Grundzeichen definiert.
Darüberhinaus ist es sinnvoll, ein Zeichen
/``,
:``,
@``,
[``,
```,
{``
Die Menge der Ergänzungszeichen soll zunächst nicht beschränkt werden,
obwohl sie die Größe der von Implementierungen genutzten
Umkodierungstabellen bestimmt. Es sind alle Zeichen mit den
Codes 33 (,,!``) bis 126 (,,~``) zugelassen.
Im Zusammenhang mit den griechischen Buchstaben tritt die Frage auf,
ob diese als Literal oder in der Verbalform verwendet werden sollen:
Also ,,der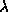 
-Kalkül`` oder ,,der Lambda-Kalkül``.
Es scheint so, als würde die Literalform eine Anfrage nur unnötig
erschweren. Katalogisierungsregeln sehen in der Regel bestmögliche
Verbalisierung vor. Ein Kompromiß könnte die Zulassung von
LaTeX-Syntax sein: \lambda-Kalk"ul. Auf diese Weise
könnten alle LaTeX-Zeichen in ihrer Verbalform in den Speicher
wandern, ohne daß die Information darüber verloren geht, daß
ein einzelnes Zeichen verwendet wurde. Auf diese Weise könnte auch in Formeln
gesucht werden. Es wird also zunächst auf eine Literalform für
griechische Buchstaben verzichtet.
Damit sich die Aufnahme von LaTeX-Syntax in das bisher beschriebene
Kodierungssystem einpaßt, ist eine Menge von Startzeichen für
LaTeX-Steuersequenzen zu definieren. Die Menge dieser Zeichen
hat als Grundzeichen einen beliebigen Buchstaben, der zugleich der
erste Buchstabe der Steuersequenz ist und als Erweiterungszeichen
,,\``. Die folgenden Zeichen der Steuersequenz werden als normale
Buchstaben kodiert, wie bereits beschrieben. Auf diese Weise sind
alle LaTeX-Steuersequenzen kodierbar, die mit einem Buchstaben
beginnen, nach ihrer Verbalform sortierbar und als Steuersequenz
oder verbal anfragbar. Das Beispiel ,,der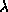 
-Kalkül`` würde also
folgendermaßen kodiert werden:
d!e!r l\a!m!b!d!a!-K!a!l!k!u"l!.
Entsprechend selektiert die Anfrage
l\a!m!b!d!a!-K!a!l!k!u"l! 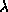-Kalkül
[lL]!a!m!b!d!a!-K!a!l!k!u"l! Lambda-Kalkül, lambda-Kalkül
[lL][\!]a!m!b!d!a!-K!a!l!k!u"l! Lambda-Kalkül, lambda-Kalkül,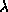-Kalkül, 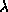-Kalkül
Bei der Übernahme von LaTeX-Texten ist zu beachten, daß viele als Steuersequenz kodierte Zeichen nur im Mathematik-Modus definiert sind.
Die vorläufige Zuordnung von Codes zu Zeichen ist in Tabelle 1 dargestellt. Die Tabelle wird vervollständigt, falls die Kodierung zum Einsatz kommen sollte.
Latin1-Codes sind an der führenden ,,00`` des Hexcodes zu erkennen.
